MiniMax & Game Playing AI

2018-07-12

1. Click on either first player or second player
2. If you choose first player click a location on the board to begin playing
3. When the game is finished click reset to clear the board

Disclaimer: I haven't implemented any exception handling so at the beginning of each game you must select a player, and at the end of each game you must hit reset, or the game logic will break.

Game playing AI's have achieved a great deal of sucess recently. I'm talking about agents like AlphaGo that are capable of defeating world class GO players, or more recently the agent from agent from OpenAI, that they call OpenAI Five. An agent trained using reinforcement learning that has begun to beat amateur human teams at the video game Dota 2. As OpenAI puts it, "Dota 2 is one of the most popular and complex esports games in the world, with creative and motivated professionals who train year-round to earn part of Dota’s annual $40M prize pool (the largest of any esports game)."

A variety of strategies and algorithms for game playing AI's and algorithms exist. AlphaGo uses a combination of reinforcement learning and Monte Carlo Tree Search, while OpenAI Five uses a reinforcement learning algorithm known as proximal policy gradients.

Algorithms for playing games have quite a long history. IBM's chess playing program Deep Blue, was one of the first well known algorithms to achieve success against a human player, defeating the chess grand master Gary Kasparov. Deep Blue used a form of tree search, where many possible sequences of games moves are calculated in advance, and the nodes of the tree, which correspond to game states, are evaluated for "goodness" in some manner.

I find game playing agents and algorithms to be very interesting, so I've started to create some of my own implementations of existing algorithms. In a previous post I implemented an Atari game playing deep q-learning algorithm. Now I've started looking into a different class of algorithms. Namely, tree search algorithms like minimax and monte carlo tree search.

The minimax algorithm, can be used for two player games like chess or tic-tac-toe. From Wikipedia, "The minimax value of a player is the smallest value that the other players can force the player to receive, without knowing the player's actions; equivalently, it is the largest value the player can be sure to get when they know the actions of the other players".

Essentially, the minimax algorithm assumes that your opponent will choose moves that minimize your own gain, while you will choose moves that maximize your gain. In a simple game like tic-tac-toe the space of possible games is small enough that every possible way a tic-tac-toe game could be played out can be enumerated in a tree.

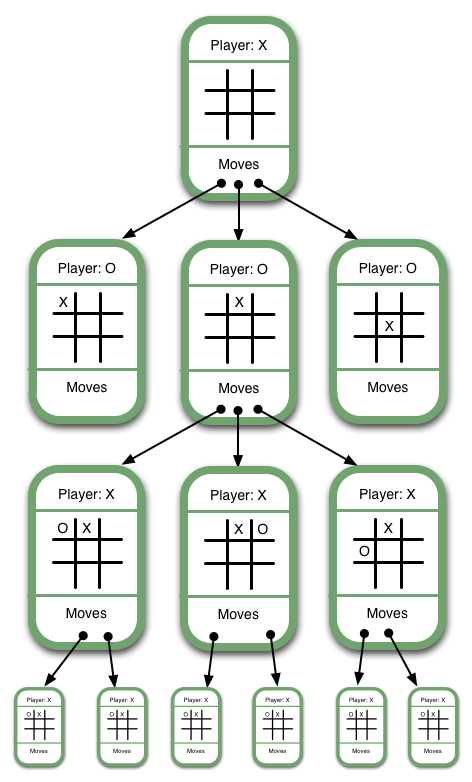
At end states (states where one player wins or there is a draw) a value can be assigned. For example a state where you win could be assigned a 1, a draw could be assigned a 0, and a loss could be assigned -1. Starting from these end states the values can be propagated back up to the root of the tree. Which values propagate depend on whose turn it is at a particular node in the tree. For example a node where it is your opponent's turn and they can make a move to win would be assigned -1 because this would result in a loss for you. This is what the mini in minimax refers to. When it is your opponent's turn the algorithm assumes they will choose a move that minimizes your gain.

Try your luck against my implementation of the minimax algorithm up above. In tic-tac-toe a player following the minimax algorithm is guaranteed to at worst draw, so if you manage to win there is a bug in my implementation.